salvador piza: marzo 2012

Asíntota

Curva: en rojo.
Asíntota: línea punteada en azul.

En matemática, se le llama asíntota a una línea recta que se aproxima continuamente a otra función o curva; es decir que la distancia entre las dos tiende a cero, a medida que se extienden indefinidamente.
También se puede decir que es la curva la que se aproxima continuamente a la recta; o que ambas presentan un comportamiento asintótico.

Historia y significado

La palabra asíntota se confunde coloquialmente con recta asintótica. Deriva del gr: ἀσύμπτωτος — asýmptōtos— “aquello que no cae”; en donde a- posee un valor privativo (= no), mientras que sym-ptōtos- connota a aquello que «cae» o «cae junto (a algo)». Se suele agregar a la definición de asíntota a una curva, el que «no se encuentran nunca».^[1] Esta interpretación intuitiva está plasmada por Apolonio de Perga, en su conocido tratado Sobre las secciones cónicas, para referirse a una recta que no interseca a una rama de una hipérbola.^[2]
En geometría, el comportamiento asintótico se refiere a una eventual propiedad entre curvas, y más precisamente, entre funciones o partes de funciones: segmentos de rectas, hojas de hipérbolas, etc. Es en este sentido que se habla de recta asintótica como tangente al infinito de una rama parabólica, o bien de curvas asintóticas.
Su estudio más profundo desborda el mero campo de aplicación de la geometría elemental y el trazado de curvas planas; con el desarrollo del álgebra y del cálculo infinitesimal, las nociones intuitivas «tiende a infinito» y «tiende a cero» se formalizan (netamente con el concepto de límite matemático), y con ello también el cálculo de asíntotas.

Gráfica de asíntotas

Las asíntotas ayudan a la representación de curvas, proporcionan un soporte estructural e indican su comportamiento a largo plazo. En tanto que líneas rectas, la ecuación de una asíntota es simplemente la de una recta, y su expresión analítica dependerá de la elección del sistema de referencias (y = m•x + b en coordenadas cartesianas).
Si bien suelen representarse en un mismo sistema de coordenadas, las asíntotas no forman parte de la expresión analítica de la función, por lo que -en numerosos ejemplos- no están incluidas explícitamente dentro de la gráfica, o bien se las indica con una línea punteada.
En muchos casos, las asíntotas coinciden con los ejes de coordenadas, es decir que sus ecuaciones en coordenadas cartesianas serán: x = 0, y = 0.
Se distinguen tres tipos:

Asíntotas verticales: rectas perpendiculares eje de las abscisas, de ecuación x = c^te.
Asíntotas horizontales: rectas perpendiculares al eje de las ordenadas, de ecuación y = c^te.
Asíntotas oblicuas: si no son paralelas o perpendiculares a los ejes, de ecuación y = m•x + b.

(Nota: c^te=constante).

Las ramas de la función tienen asíntotas.

Los ejes son las asíntotas.

Las ramas de la función tienen asíntotas.

Comportamiento asintótico entre una curva y una recta.

Determinación analítica de asíntotas

En análisis, cálculo y geometría analítica, el comportamiento de funciones no triviales en las cercanías de puntos de «indefinición» (tales como la división por cero o las formas indeterminadas), aportan información valiosa sobre su gráfica, y en este contexto las asíntotas surgen naturalmente como «soluciones» (o direcciones) en estos puntos. En este sentido, una función puede tener una «asíntota por la derecha» pero no por la izquierda (o viceversa); o bien una recta puede intersecar a una curva en un número finito (o infinito) de puntos, y presentar de todos modos un comportamiento asintótico.

Cálculo de asíntotas por medio de límites

Véase también: Límite matemático

Asíntota vertical

Se llama Asíntota Vertical de una rama de una curva y = f(x), a la recta paralela al eje y que hace que la rama de dicha función tienda a infinito. Si existe alguno de estos dos límites:

$\lim_{x \to a^-} f(x) = \pm\infty$

$\lim_{x \to a^+} f(x) = \pm\infty$

a la recta x = a se la denomina asíntota vertical.
Ejemplos: logaritmo neperiano, tangente

Asíntota horizontal

Se llama Asíntota Horizontal de una rama de una curva y = f(x) a la recta paralela al eje x que hace que la rama de dicha función tienda a infinito. Si existe el límite:

$\lim_{x \to \pm\infty} f(x)= a$ , siendo a un valor finito

la recta y = a es una asíntota horizontal.
Ejemplos: función exponencial, tangente hiperbólica

Asíntota oblicua

La recta de ecuación y = mx + b (m ≠ 0) será una asíntota oblicua si: $\lim_{x \to \pm\infty}f(x)-(mx+b) = 0$ .

Los valores de m y de b se calculan con las fórmulas: $m = \lim_{x \to \pm\infty}{f(x) \over x}$ ; $b = \lim_{x \to \pm\infty}{f(x)-mx}$ .

Asíntotas de funciones racionales

Véase también: Función racional

En la representación gráfica de una función racional juega un papel esencial, cuando existen, las asíntotas. Si bien es posible aplicar el método por límites descrito anteriormente, en el caso de funciones racionales, suelen utilizarse técnicas algorítmicas que no precisan del análisis matemático.Una función racional puede tener más de una asíntota vertical, pero solo una que sea horizontal u oblicua (es decir que si tiene asíntota horizontal entonces no puede tener asíntota oblicua, y viceversa).

El dominio de la función determina las asíntotas verticales.
La división de polinomios proporciona las asíntotas horizonales u oblicuas.

$y = \frac{1}{x}$

Para mayor claridad, sea:

$\frac{A(x)}{B(x)}= \frac{a_mx^m+a_{m-1}x^{m-1}+...+a_1x+a_0}{b_nx^n+b_{n-1}x^{n-1}+...+b_1x+b_0}$

Si $m<n \,$ , hay una asíntota horizontal de ecuación: y = 0.
Si $m=n \,$ , hay una asíntota oblicua de ecuación: y = a_m/b_n (el cociente de los coeficientes principales).
Si $m>n \,$ , no hay asíntota horizontal; si el grado del numerador es exactamente uno más que el denominador, hay una asíntota oblicua, y su ecuación viene dada por el cociente de la división de los polinomios.
Las asíntotas verticales se dan en los valores que anulan el denominador pero no el numerador. Si hay una raíz en común, se compara la multiplicidad de las raíces.
Ejemplos:

La función homográfica $f(x) = \frac{a x + b}{c x + d}$ tiene dos asíntotas, AV: x = -d/c , AH: y = a/c
En el caso particular $y = \frac{1}{x}$ las asíntotas son los propios ejes cartesianos.

Asíntotas de curvas polares

Las asíntotas a una curva descrita por una ecuación en coordenadas polares $r = \rho(\theta)\$ , son las curvas que se obtienen cuando r o θ tienden a infinito o hacia un valor dado.

Recta asintótica

Una curva polar tendrá una dirección asintótica cuando, para $\theta_0\$ dado,

$\lim_{\theta\to \theta_0} \rho(\theta) = \infty$ .

La curva tiene entonces una recta asintótica si existe un real λ tal que

$\lim_{\theta\to \theta_0} \rho(\theta)sin(\theta-\theta_0)=\lambda$

y se acerca a la recta de ecuación

$\rho(\theta) = \frac{\lambda}{sin(\theta-\theta_0)}$ .

Círculo asintótico

Una curva polar tendrá un círculo asintótico si existe un $\rho_0\$ dado, tal que

$\lim_{\theta\to \infty} \rho(\theta) = \rho_0$ .

La curva se enrolla sobre el círculo de ecuación $\rho = \rho_0\$
Si en la vecindad de θ $\rho(\theta)\ < \rho_0\$ entonces la curva se enrolla al interior del círculo asintótico; inversamente, si $\rho(\theta)> \rho_0\$ , entonces se enrolla al exterior.

Ejemplos

Las más variadas funciones evidencian del comportamiento asintótico: desde el simple gráfico de una curva plana en dos dimensiones, hasta superficies tridimensionales más complejas; tanto en funciones algebraicas (polinómicas, racionales) como trascendentes (trigonométricas, logarítmicas, exponenciales), ya sea en coordenadas cartesianas, polares, etc.
Las asíntotas actúan como curvas guía para graficar otras curvas, o funciones.

Funciones racionales

Función racional con Asíntota Oblicua
y dos Asíntotas Verticales

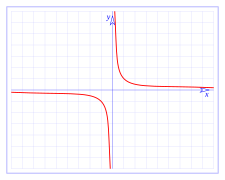
Función racional con Asíntota Horizontal
y dos Asíntotas Verticales

Funciones trascendentes

tan(x)
Asíntotas verticales cada π/2.

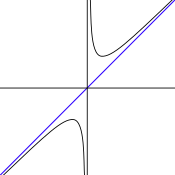
ln(x)
Asíntota vertical hacia abajo.

exp(x)
Asíntota horizontal a la izquierda.

Curvas polares

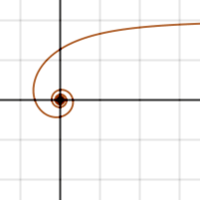
Espiral inversa de Arquímedes Asíntota en .

Espiral inversa de Arquímedes

$r \theta = a \$

Asíntota en $y = a \$ .

Curva de Kappa

Folium de Descartes
$r(\theta) = \frac{3 a \sin \theta \cos \theta}{\sin^3 \theta + \cos^3 \theta }$

Asíntota en $x + y + a = 0 \$ .

Curvas asintóticas

Tridente de Newton:
$x y = ax^3+ bx^2 + cx + d\,$ .

Asíntotas: la parábola de ecuación $\,y = a x^2 + b x + c$ ,
y la hipérbola de ecuación $y = \frac{d}{x}$ .